|
|
computer graphics tutorials
|
coordinate systemsThese are the coordinate systems a 3D vertex is transformed thru: Transformation of a 3D vertex thru coordinate systems:
local
Green indicates transformations done by engine. local coordinate system3D objects have their own local coordinate system. Also known as object coordinates. world coordinate systemWorld coordinate system contains simulated world (scene to be rendered). It is mapped to eye coordinate system by eye matrix. eye coordinate systemEye coordinate system stays mapped to view-port of window system. Eye vertexs are final result of all transformations, which are submitted to gfx-sys. (X,Y) eye coordinates correlate to (X,Y) view-port coordinates. An eye Z coordinate measures distance from eye/view-point. For an eye vertex, (X,Y) are divided by Z to project vertex onto view-port (window). This projection creates illusion of perspective on a 2D computer display. perspective coordinate systemEye coordinates are transformed by underlying graphics system into perspective coordinates. View frustrum (which exists in eye space) is mapped to perspective coordinates. view-port coordinate systemThis is 2D window on computer's window system. normal coordinate systemA normal vector calculated by a cross product exists in its own coordinate system where its origin is one of vertexs on a polygon on which it is normal/perpendicular to. |
transpose matrixA matrix maps one coordinate system to another. Mapping is directed. Mapping can be reversed by transposing a matrix. This is done by turning each row into a column. Note: transpose matrix and inverse matrix are different mathematical concepts. [ Xx Xy Xz ] [ Xx Yx Zx ] [ Yx Yy Yz ] [ Xy Yy Zy ] [ Zx Zy Zz ] [ Xz Yz Zz ] An application of a transpose matrix is animated firing guns in a 1st-person view. Eye matrix maps world-to-eye coordinates. Tracer rounds from gun are modeled starting from a local coordinate system. What is needed is a local matrix that maps local-to-world coordinates and it must be aligned with eye matrix. Transpose of eye matrix can be used as local matrix. Although transposed eye matrix apparently maps eye-to-world coordinates, it will work as result of transformation is in world coordinates (on output side). Local coordinates are substituted for eye coordinates on input side. A copy of eye matrix used as local matrix would not work because two transformations from local-to-world and world-to-eye would nonsensically pass thru eye matrix (which is meant for latter transformation only). |
BSP trees"BSP" usually refers to an AA-BSP tree. overviewTwo kinds of BSP trees are axis-aligned and polygon-aligned (AA-BSP and PA-BSP). A BSP node has two child nodes metaphorically named left and right. axis-aligned BSP treesAxis-aligned is much simpler and faster to construct than polygon-aligned. Axis-aligned is useful for containing 3D objects in rectangular volumes. Objects can be coarsely (imprecisely) sorted in back-to-front order by traversing an axis-aligned using distance between a partition vs. view-point as criteria for branching left or right. Granularity of sorting is rectangular volume of a BSP node. A BSP node may contain multiple Objects, but sorting (by BSP traversal) goes no further (this is why sorting isn't precise). Bypassing finely sorting Objects of a BSP node is possible if none of Objects are translucent. Rendering opaque objects out-of-order relies on hardware Z buffer. Note that purpose of sorting is to properly alpha-blend translucent Objects. polygon-aligned BSP treesPolygon-aligned BSP trees are well-suited for precise collision-detection of objects having irregular shapes. Though they have disadvantages such as being complex and slow to construct. Polygons intersecting a plane must be split into two polygons. traversal path of BSP varies according to view-pointKey to understanding a BSP tree is that traversal path varies according to a branch condition and a stop condition. Unlike a regular binary tree, these conditions are variable. For example, when adding Objects, branch condition is whether an Object can fit inside a partition. When culling/sorting, branch condition is determined by distance and orientation of a partition relative to view-point culling and sorting objects by traversingCulling and sorting objects are done simultaneously by traversing a BSP tree. Traversing is sorting. Reaching a stop condition that evaluates true is culling. A BSP node and its descendants outside view frustum are culled since they won't be visible. This culling method is efficient, since a whole subtree of invisible objects are eliminated in one step. To properly render translucent polygons, furthest-to-nearest order is necessary. During traversal, if two partitions are visible, partition that is furthest from view-point is selected. A partition's distance and whether inside frustrum are sub-conditions of branch condition. Target of traversal path is to reach smallest and most distant partition. Branch condition determines which ways to branch:
If left is farther than right from view-point:
If left is facing, branch.
If right is facing, branch.
If right is farther than left from view-point:
If right is facing, branch.
If left is facing, branch.
Stop condition determines when to stop recursing:
Ignoring view frustrum for a moment, possibly all partitions or none will be visible. For example, if view-point is at corner of a partition and facing outwards, then none are visible. If view-point is rotated 180 deg, then all become visible. adding objects to a BSP TreeAdding objects to a AA-BSP is similar to octrees. Tree is recursed until a node (corresponding to an octant) is found that object doesn't fit or maximum depth is reached, then object is attached to its parent node. objects which intersect a BSP PlaneThere are several cases where an Object can intersect a BSP plane. One case is a Dyna that moves between any two partitions. Worst case is a very large Object that, besides intersecting one or more planes, overlays partitions in multiple BSP trees. A way to solve intersection is to let multiple BSP nodes reference same Object in case Object occupies at least one partition that wasn't culled, but keep a flag (or frame number) to remember that Object was drawn in a frame in case one or more of its partitions are visible (to avoid redraw). collision-detection using a polygon-aligned BSP treeTesting if a 3D vertex is inside a PA-BSP is done by traversing. If vertex is inside, then vertex will be behind every polygon encountered during traversal. Eventually, traversal will stop at a leaf node, which means a collision was detected. |
minimum distance between point and line segment
AB is line SEGMENT.
Shortest line from a point to a line is an orthogonal line. Orthogonal line intersects at a tangent. If orthogonal line were rotated in either direction, it would move off other line and would have to be increased to remain in intersection, thus it is has minimum distance.
A-------------B
|
|
C
According to linear algebra, dot product can be used to compute a projection of vector onto another vector. In this case, projection of C onto AB.
AC . AB
t = --------------
||AB|| * ||AB||
DotProduct( AC, AB )
t = --------------------
DistanceSquared( B ) = DotProduct( AB, AB )
t is a scalar that can be used to compute point of intersection I: I = A + t * (B - A) computer implementation:Goal is find minimum distance on a point on LINE SEGMENT. If intersection is outside LINE SEGMENT, then instead, compute distances between CA and CB and return minimum. This C++ code is meant for testing/demonstration. It is implemented as a class/object as a lot of results are computed which are stored in data members (too complex for a function's return value). C++ code implementation:(written by Jim Brooks)
////////////////////////////////////////////////////////////////////////////////
///
class DistancePointLineSegment
{
public:
/*****************************************************************************
* This constructor is minimum distance function.
*****************************************************************************/
DistancePointLineSegment( const Vector2& a,
const Vector2& b,
const Vector2& c )
{
// AC and AB are vectors with A as origin.
// Compute orthogonal projection of C onto AB as scalar t.
const Vector2 ac( c - a );
const Vector2 ab( b - a );
mT = DotProduct( ac, ab )
/ DotProduct( ab, ab );
// If intersection is on line SEGMENT (within A..B),
// then t = {0,..,1}.
if ( (mT >= 0.0f) and (mT <= 1.0f) )
{
mIfIntersectsLineSegment = true;
mIntersection.x = a.x + mT * (b.x - a.x);
mIntersection.y = a.y + mT * (b.y - a.y);
mDistance = Distance( mIntersection - c );
}
else
{
// Intersection is outside line SEGMENT.
// Instead, compute distances between CA and CB
// and return minimum.
mIfIntersectsLineSegment = false;
//mIntersection.x = N/A
//mIntersection.y = N/A
mDistance = std::min( Distance( c-a ), Distance( c-b ) );
}
}
public:
bool mIfIntersectsLineSegment; ///< true if intersection on LINE SEGMENT (false if outside segment)
fp mT; ///< always valid
Vector2 mIntersection; ///< N/A if not mIfIntersectsLineSegment
fp mDistance; ///< minimum distance between point C and line segment AB
};
Test results: ---------------------------------------- Diagonal line from +Y to -X. Midpoint/intersection is obvious. line = Vector2:(0,500) Vector2:(-500,0) point = Vector2:(0,0) t = 0.5 distance = 353.553 intersection = Vector2:(-250,250) ---------------------------------------- Horizontal line that spans -X..+X. Intersection is obvious. line = Vector2:(-50,50) Vector2:(50,50) point = Vector2:(0,0) t = 0.5 distance = 50 intersection = Vector2:(0,50) ---------------------------------------- Diagonal thru origin. line = Vector2:(-50,50) Vector2:(100,-100) point = Vector2:(0,0) t = 0.333333 distance = 0 intersection = Vector2:(0,0) ---------------------------------------- Diagonal aiming at origin but halfway there. line = Vector2:(-50,50) Vector2:(-25,25) point = Vector2:(0,0) t = 2 distance = 35.3553 intersection = none ---------------------------------------- Diagonal aiming at origin but halfway there (swap a,b). line = Vector2:(-25,25) Vector2:(-50,50) point = Vector2:(0,0) t = -1 distance = 35.3553 intersection = none ---------------------------------------- Directly aims at origin but does not quite reach. line = Vector2:(-50,-50) Vector2:(-0.1,-0.1) point = Vector2:(0,0) t = 1.002 distance = 0.141421 intersection = none ---------------------------------------- Directly aims at origin but does not reach (swap a,b). line = Vector2:(-0.1,-0.1) Vector2:(-50,-50) point = Vector2:(0,0) t = -0.00200401 distance = 0.141421 intersection = none ---------------------------------------- Skewed above origin towards NE. line = Vector2:(-100,10) Vector2:(100,500) point = Vector2:(0,0) t = 0.0539093 distance = 96.3637 intersection = Vector2:(-89.2181,36.4156)
References: |
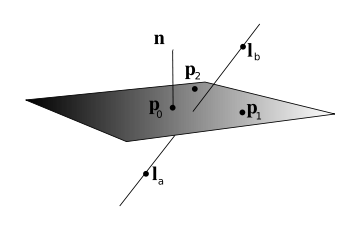
line-plane intersectionThis requires thinking in terms of algebra and finding value of a variable. Known is a plane defined by its position and its normal vector. And known is a line segment defined by two vectors for its end points.
Thinking logically, there is a point on line that has to intersect plane (ignore other cases for now).
Idea is that there is a distance from line's beginning to its end.
If a line's normalized direction is multiplied by this distance, that produces line's end-point.
Likewise, a line's normalized direction can be multiplied an unknown variable
C++ code implementation:(written by Jim Brooks)
/*******************************************************************************
*
*******************************************************************************/
bool IntersectionPlaneLine( Vector3& intersection, // OUT
const Vector3& planePos,
const Vector3& planeNormalVector,
const Vector3& lineBegin,
const Vector3& lineEnd )
{
// Based on:
// Algrebraic form
// https://en.wikipedia.org/wiki/Line-plane_intersection
// doc/html/math/linePlaneIntersection.html
//
// Idea is to find value of factor d
// which can be used to multiplied line direction (distance from line)
// to a point on line that intersects plane.
//
// Express plane as equation:
// (p - p0) . n = 0
// n is plane's normal vector
// p0 is a given point on plane
// p is a variable to be solved, in this case, point of intersection
//
// p = d*l + l0
// l is a direction vector of line
// l0 is a point on line
// In this C++ function
// ld = Normalize( lineEnd - lineBegin )
// l0 = lineBegin
//
// Substitute line into plane equation:
// ((d*l + l0) - p0) . n = 0
//
// Distribute n:
// d*l . n + (l0 - p0) . n = 0
//
// Solve for d (line factor):
// (p0 - l0) . n
// d = -------------
// l . n
//
// If line is parallel and outside plane: 0 / non-zero
// If line is parallel and on plane : 0 / 0
// Else intersection and d represents distance along line from l0
const Vector3& p0 = planePos; // alias for math
const Vector3& l0 = lineBegin; // alias for math
const Vector3& n = planeNormalVector; // alias for math
const Vector3 l = Normalize( lineEnd - lineBegin ); // line direction, unit
const fpx numerator = DotProduct3( p0 - l0, n );
const fpx denominator = DotProduct3( l, n );
if ( ABS(denominator) < 0.0001 )
{
return false;
}
else
{
const fpx d = numerator / denominator;
intersection = lineBegin + (l * d);
return true;
}
}
References: |
collision detectionFor small objects, simple calculations based on bounding box or spheres should suffice. For objects that are large and have irregular shapes, polygon-aligned BSP trees are necessary to accurately detect collisions. If collider is a small object and its rate of translation is fine enough, a simple point intersection test of collidable's BSP tree should suffice. |
|
|
 world
world  perspective
perspective